It’s Pi Day 2025
Archimedes calculated the perimeter of inscribed regular polygons within a circle to approximate the value of π.
A square inscribed in a unit circle can be divided into four right triangles with two sides of unit length, corresponding to the radius of the circle. The third side can be calculated by Pythagoras’ theorem to be √2. The perimeter of the square would be 4√2. Given, C=πd, we can calculate π from the circumference by dividing it by the diameter, 2, giving 2√2.
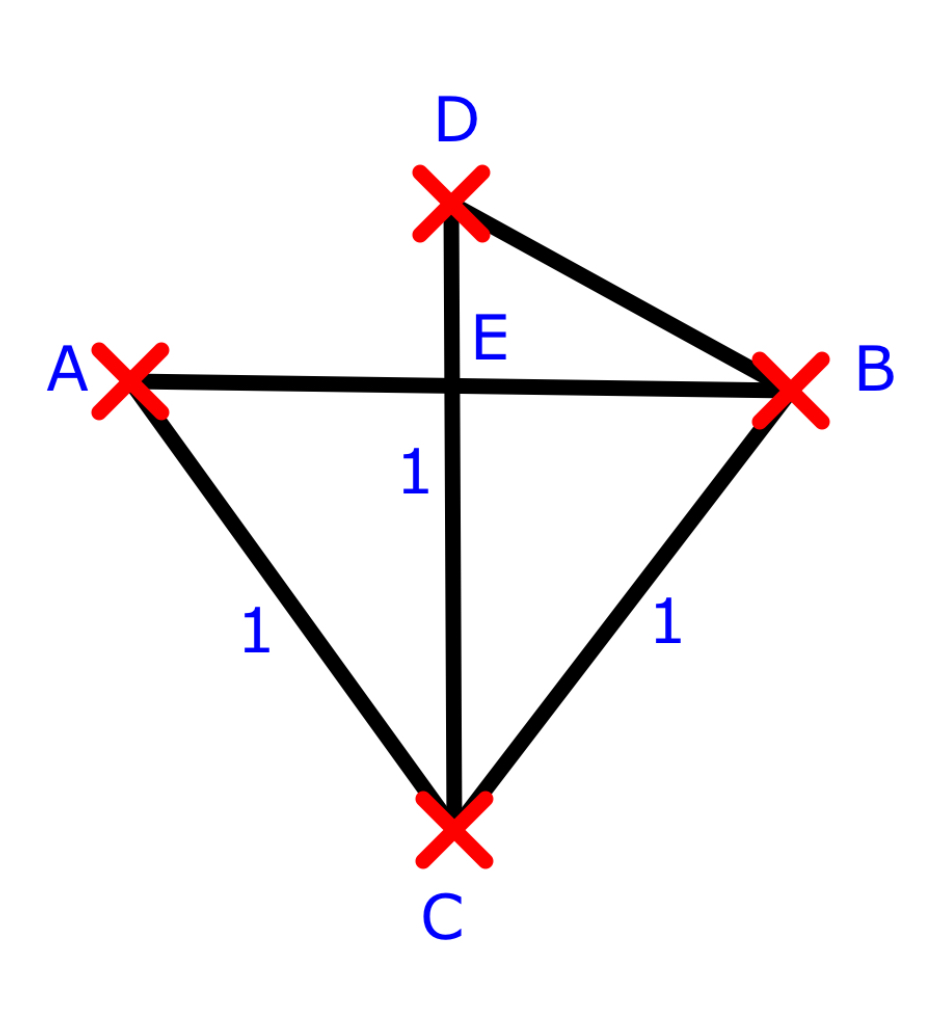
CA, CD and CB are all the unit radius. AB is √2 as calculated above. The angle ACB can be bisected with the line CD. EB is half of AB. Using Pythagoras’ theorem on the triangle BCE we can calculated CE. DE is then 1 - CE, allowing us to use Pythagoras’ theorem for a final time on BDE to calculated BD. The improved approximation of the perimeter is now 8 x BD.
We can iterate on this process using the following code:
let rec pi edge_squared sides = function
| 0 -> sides *. Float.sqrt(edge_squared) /. 2.
| n ->
let edge_squared = 2. -. 2. *. Float.sqrt (1. -. edge_squared /. 4.) in
let sides = sides *. 2. in
pi edge_squared sides (n - 1)
let approximation = pi 2. 4. 13
let () = Printf.printf "pi %.31f\n" approximation
I found this method quite interesting. Usually, as the number of iterations increases the approximation of π becomes more accurate with the delta between each step becoming smaller until the difference is effectively zero (given the limited precision of the floating calculation). However, in this case, after 13 iterations the approximation becomes worse!
| iteration | approximation | % error |
|---|---|---|
| 0 | 2.8284271247461902909492437174777 | 9.968368 |
| 1 | 3.0614674589207178101446515938733 | 2.550464 |
| 2 | 3.1214451522580528575190328410827 | 0.641315 |
| 3 | 3.1365484905459406483885231864406 | 0.160561 |
| 4 | 3.1403311569547391890466769837076 | 0.040155 |
| 5 | 3.1412772509327568926096319046337 | 0.010040 |
| 6 | 3.1415138011441454679584239784162 | 0.002510 |
| 7 | 3.1415729403678827047485810908256 | 0.000627 |
| 8 | 3.1415877252799608854161306226160 | 0.000157 |
| 9 | 3.1415914215046352175875199463917 | 0.000039 |
| 10 | 3.1415923456110768086091411532834 | 0.000010 |
| 11 | 3.1415925765450043449789063743083 | 0.000002 |
| 12 | 3.1415926334632482408437681442592 | 0.000001 |
| 13 | 3.1415926548075892021927302266704 | -0.000000 |
| 14 | 3.1415926453212152935634549066890 | 0.000000 |
| 15 | 3.1415926073757196590463536267634 | 0.000001 |
| 16 | 3.1415929109396727447744979144773 | -0.000008 |
| 17 | 3.1415941251951911006301543238806 | -0.000047 |
| 18 | 3.1415965537048196054570325941313 | -0.000124 |
| 19 | 3.1415965537048196054570325941313 | -0.000124 |
| 20 | 3.1416742650217575061333263874985 | -0.002598 |
| 21 | 3.1418296818892015309643284126651 | -0.007545 |
| 22 | 3.1424512724941338071005247911671 | -0.027331 |
| 23 | 3.1424512724941338071005247911671 | -0.027331 |
| 24 | 3.1622776601683795227870632515987 | -0.658424 |
| 25 | 3.1622776601683795227870632515987 | -0.658424 |
| 26 | 3.4641016151377543863532082468737 | -10.265779 |
| 27 | 4.0000000000000000000000000000000 | -27.323954 |
| 28 | 0.0000000000000000000000000000000 | 100.000000 |
Using the decimal package we can specify the floating point precision we want allowing us to get to 100 decimal places in 165 steps.
open Decimal
let context = Context.make ~prec:200 ()
let two = of_int 2
let four = of_int 4
let rec pi edge_squared sides n =
match n with
| 0 -> mul ~context sides (div ~context (sqrt ~context edge_squared) two)
| n ->
let edge_squared =
sub ~context two
(mul ~context two
(sqrt ~context (sub ~context one (div ~context edge_squared four))))
in
let sides = mul ~context sides two in
pi edge_squared sides (Int.pred n)
let () = pi two four 165 |> to_string ~context |> Printf.printf "%s\n"
This code is available on GitHub